Mathematik-Download
- Liste 
|
Mathematik-Download
- Liste |
|
|
Alle Dateien können frei heruntergeladen werden. |
Art |
(EX)...Excel-Programm (GEO)...Geogebra-Programm (WORD)...Word-Dokument (PDF)...als (La)Tex-Dokument (PY)...Python-Programm |
| Kurzbeschreibung | Was steht im Programm? | Download |
|
Das Buffon'sche Nadelproblem
|
Die experimentelle Bestimmung von p durch Werfen von Nadeln aus dem Jahre 1777 von Graf George de Buffon.
Eine theoretische Herleitung liegt als Word-Dokument vor! (GEO),(WORD) |
Download |
|
Konfidenzintervall bestimmen
|
Eine Konfidenzellipse gibt das Vertrauensintervall bei einer Schätzung von der Stichprobe auf die Gesamtheit an. Eine theoretische Herleitung der Konfidenzellipse liegt als Word-Dokument vor!(GEO),(WORD) | Download |
|
Binomialverteilungenn
|
Mit dem Programmm können Wahrscheinlichkeiten von Binomialverteilungen ermittelt werden. Auch eine Approximation der Binomialverteilung durch die Normalverteilung unter Berücksichtigung des Stetigkeitskorrektursummanden ist möglich.(GEO) | Download |
|
Normalverteilungen
|
Mit dem Programmm können Wahrscheinlichkeiten von Normalverteilungen und Radien von Sigma-Umgebungen ermittelt werden. Als Berechnungsgrundlage dient die Gauss'sche Glockenkurve.(GEO) | Download |
|
p-Bestimmung durch die Monte-Carlo-Methode
|
Die experimentelle Bestimmung von p durch Werfen von Punkten in ein Quadrat. Eine theoretische Herleitung liegt als Word-Dokument vor! (GEO),(WORD) | Download |
|
2 Punkte setzen auf eine Strecke
|
Wie groß ist die Wahrscheinlichkeit, wenn man auf einem Band 2 beliebige Punkte setzt und daraus ein Dreieck entstehen soll? Eine theoretische Herleitung liegt als Word-Dokument vor! (EX),(WORD),(GEO) | Download |
| Pfannkuchen mit Senf
|
Von neun Pfannkuchen ist einer Senf gefüllt. Mit welcher Wehrscheinlichkeit bekommt man diesen Pfannkuchen, wenn abwechselnd gezogen wird.(WORD) | Download |
| Geburtstagsproblem
|
Ab wie viel Personen ist die Wahrscheinlichkeit größer als 50%, dass mindestens 2 Personen an einem Tag (Monat) Geburtstag haben? Eine theoretische Herleitung liegt als Word-Dokument vor! (EX),(WORD) | Download |
Kantinentreff
 |
Mit welcher Wahrscheinlichkeit sieht Robert jeden Mittag Cornelia? Mehrere Lösungsmöglichkeiten für das gleiche Problem werden gezeigt.(PDF),(GEO) | Download |
| Gummibärenproblem
|
Es werden aus einer Tüte Gummibärchen gezogen. Die Bärchen treten in sechs Farben auf, von einer Farbe sind sogar doppelt so viel vorhanden, wie von den anderen. Wie oft muss man in die Tüte hineingreifen, damit man von jeder Farbe genau ein Gummibärchen zieht.(GEO) | Download |
| Würfelspiel
|
Es befinden sich N Würfel in einem Becher. Jeder Würfel, der eine Sechs zeigt, wird beiseite gelegt. Die übrigen Würfel werden erneut ausgeschüttet. Dies geschieht so lange, bis jeder Würfel oben eine Sechs zeigt. Wie lange dauert das Spiel im Mittel?(GEO) | Download |
| Alice und Bob, eine beeindruckendes Münzwurfspiel
|
Alice und Bob werfen eine Münze mit der Aufschrift 0 und 1. Wie oft muss man die Münze werfen, damit auf eine 0 eine 0 folgt, wie oft muss man werfen, damit auf eine 0 eine 1 folgt.(GEO) | Download |
| Seitenlängen eines Dreiecks würfeln
|
Die drei Seitenlängen eines Dreiecks werden mithilfe eines Würfels ermittelt. Mit welcher Wahrscheinlichkeit lässt sich aus diesen Seitenlängen eines Dreiecks konstruieren?(GEO) | Download |
| Mäusejagd
|
Eine Katze versucht, mithilfe eines Würfels, eine Maus im Koordinatensystem zu fangen. Mit welcher Wahrscheinlichkeit passiert dies?(GEO),(PY) | Download |
| Äpfel im Keller
|
Aus einem dunklen Keller werden zwei Äpfel einem Korb zufällig entnommen. Die Anzahl der Äpfel im Korb ist gesucht.(PDF),(GEO),(PY) | Download |
| Rothschilds Töchter
|
In einer Stadt trifft man zwei blauäugige Töchter der Familie Rothschild. Die Anzahl aller Töchter Rothschilds ist gesucht, eine Aufgabe zur negativen Pellschen Gleichung. (PDF),(GEO),(PY) | Download |
| Ameisenirrläufer
|
Eine Ameise startet im Koordinatenursprung und geht mit jedem Schritt eine Längeneinheit entweder zufällig nach oben, unten, links oder rechts. Wie viel Schritte sind durchschnittlich zu erwarten bis |x|+|y|=3. Ein Programm simuliert den Weg der Ameise.(GEO) | Download |
| Erwartungswerte der Doppelsechs
|
Welches Ereignis ist eher zu erwarten, das Werfen eines Würfels, so dass zweimal hintereinander eine "6" kommt oder das Werfen zweier Würfel mit dem Ergebnis Pasch "6". Ein Programm simuliert einzeln beide Ereignisse.(GEO) | Download |
| Kurzbeschreibung | Was steht im Programm? | Download |
|
Fibonacci-Zahlen und |
Gemeinsamer Grenzwert wird bestimmt! (WORD) | Download |
|
Begrenztes Wachstum und begrenzte Abnahme, |
Theorie und Beispielaufgaben mit Lösungen! (WORD) | Download |
Additionstheoreme |
16 der wichtigsten Additiontheoreme nachgewiesen. (WORD) | Download |
Steckbriefaufgaben |
Gesucht sind Funktionsgleichungen ganzrationaler Funktionen 3., 4. und 5.Grades. Das Programm liefert dies nach Eingabe von Punkten der Funktion. (GEO) | Download |
Trassierung |
Knick- und krümmungsruckfreie Übergange werden an einem Beispiel gezeigt. Das Programm liefert entsprechende Funktionsgleichungen. (GEO) | Download |
|
|
Zwei Beispielaufgaben zur vollständigen Induktion gerechnet. (WORD) | Download |
|
|
Wie kann man einen periodischen Dezimalbruch in einen gemeinen Bruch umwandeln? Hier ein Algorithmus! (WORD) | Download |
|
Beispielaufgabe zur Berechnung eines linearen Gleichungssystems mit Hilfe von Determinanten. (WORD) | Download |
|
Für welche natürliche Zahl n ist die Summe zweier aufeinanderfolgender Quadratzahlen gleichzeitig die Summe aus einer Quadratzahl und dem Doppelten der nachfolgenden Quadratzahl? (GEO) | Download |
|
Herleitung der Heronschen Dreiecksformel. (WORD) | Download |
|
Integrale von einigen gebrochen rationalen Funktionen, Wurzelfunktionen und trigonometrischen Funktionen werden per Hand berechnet. (WORD) | Download |
|
Fläche von unendlich vielen Quadraten ist endlich |
Ein Quadrat wird in immer kleinere Quadrate zerlegt, manche davon werden gefärbt. Welche Fläche nehmen die unendlich vielen grünen Quadrate ein? (WORD),(GEO) | Download |
|
ggT und kgV-Bestimmung, befreundete Zahlen |
Das Programm liefert den größten gemeinsamen Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) zweier natürlicher Zahlen und untersucht, ob diese beiden Zahlen zueinander befreundet sind. (GEO) | Download |
|
Fröhliche Zahlen |
Das Programm findet die ersten hundert fröhlichen Zahlen. (GEO) | Download |
|
Primzahl-Bestimmung |
Das Programm gibt alle Primzahlen bis zu einer selbst benannten Grenze aus! (GEO) | Download |
|
Primzahlzwillinge, Primzahldrillinge suchen |
Das Programm sucht nach Primzahlzwillingen (p und p+2),ein anderes Programm nach Primzahldrillingen (p,p+2,p+6) bzw. (p,p+4,p+6). (GEO) | Download |
|
n*HAUS=DORF |
Für welches n gilt: n*HAUS=DORF, wobei für jeden Buchstaben eine andere Ziffer steht? Es gibt 184 Lösungen.(GEO) | Download |
|
(TOR)2=RETTER |
Für welche dreistellige Zahl ist ihr Quadrat eine symmetrische sechsstellige Zahl, wobei für gleiche Buchstaben gleiche Ziffern stehen? Es gibt nur eine Lösung. (EX) | Download |
|
32 Zahlen anordnen |
Die Zahlen 1-32 sollen so in einem Kreis angeordnet werden, dass je zwei benachbarte Zahlen Quadratzahlen sind. Es gibt nur eine Lösung. (PDF),(GEO) | Download |
|
Mordfall |
Der Todeszeitpunkt eines Mordes wird mit Hilfe einer e-Funktion festgestellt. (PDF),(GEO) | Download |
|
Fünf Zahlenstreifen |
Zahlen von 1 bis n werden auf einen Papierstreifen geschrieben, der danach in fünf Teile zerschnitten wird. Wie heißt n, wenn die Durchschnitte der einzelnen Teile bekannt sind? (PDF),(EX) | Download |
|
Fünfstellige Palindrom- |
Welche fünfstelligen Palindromzahlen sind durch 11 teilbar? (PDF),(EX) | Download |
|
Überlebenskampf von Chamäleons |
Insgesamt sieben Chamäleons in drei Farben paaren sich und wandeln sich in eine andere Farbe um, Welche Farbe bleibt über? Eine theoretische Herleitung und ein Python-Programm ermittelt die Gewinnerfarbe.(PDF),(PY) | Download |
|
Überlebenskampf von Fröschen |
Jetzt paaren sich viele verschiedenfarbige Frösche und nehmen eine andere Farbe an, ein Frosch stirbt aber dabei. Eine theoretische Herleitung und ein Python-Programm ermittelt wieder die Gewinnerfarbe. (PDF),(PY) | Download |
|
Dartscheibe |
Die Summe der Differenzen zweier nebeneinanderliegender Dartfelder beträgt bei einem Wettkapfboard 198. Eine noch größere Differenz wird ermittelt.(PDF),(EX) | Download |
|
Primzahlen mit 666 |
Eine einzige Formel in Geogebra findet alle fünfstelligen Primzahlen, in deren Mitte die Zahl 666 steht.(PDF),(GEO) | Download |
|
Goniometrische Gleichung |
Eine goniometrische Gleichung wird gelöst, die viele Scheinlösungen hat.(PDF),(GEO) | Download |
|
Quadrate von 1 bis 17 im Rechteck |
Quadrate mit einer Seitenlänge von 1 bis 17 sollen in ein 39x46 Rechteck gelegt werden. Ein Python-Programm hilft bei der Bestimmung der Anzahl der Möglichkeiten.(PDF),(GEO),(PY) | Download |
|
Zahlen und ihre Quadrate als Palindrom |
Zwei- und dreistellige Zahlen und ihre Quadrate sind Palindrome. Ein Python-Programm ermittelt sie.(PDF),(PY) | Download |
|
Aufeinanderfolgende Primzahlenpalindrome |
Bis 100.000 ermittelt ein Python-Programm aufeinanderfolgende Primzahlenpalindrome.(PDF),(PY) | Download |
|
kte Potenz |
Für welche positiven natürlichen Zahlen k kann die Summe von k aufeinanderfolgenden natürlichen Zahlen die k-te Potenz einer natürlichen Zahl sein?(PDF),(PY) | Download |
|
Rätsel des Staubsaugervertreters |
Das Alter dreier Töchter als Produkt dreier Zahlen wird gesucht.(PDF),(PY) | Download |
|
Vierstellige Pin |
Das Produkt von fünf Primzahlen ergibt eine vierstellige Pin. Ein Primzahlliste wird mit Python generiert.(PDF),(PY) | Download |
|
Summe gleich 100 |
Die Summe aufeinanderfolgender natürlicher Zahlen soll 100 ergeben. Wie viele Möglichkeiten gibt es? Ein Python Programm findet auch Zahlen, wo die Summe z.B 5000 ist.(PDF),(PY) | Download |
|
Maximales Volumen eines Quaders |
Wie müssen die Seitenlängen a, b, c eines Quaders sein, damit sein Volumen maximal wird, wenn a+b+c=12? Aufgabe mit partiellen Ableitungen und Hesse-Matrix.(PDF),(PY) | Download |
|
Maximales Quadrat im spitzwinkligen Dreieck |
Wie muss in einem spitzwinkligen Dreieck ein Quadrat einbeschrieben werden, damit sein Flächeninhalt maximal wird? Die Aufgabe wird gelöst und animiert.(PDF),(GEO) | Download |
| Kurzbeschreibung | Was steht im Programm? | Download |
| Flächeninhalt einer Ellipse |
Der Flächeninhalt einer Ellipse in Mittelpunktlage wird mit einem Integral berechnet. (WORD) | |
| Lagebeziehungen von Punkten, Geraden und Ebenen |
Lagebeziehungen von Punkten, Geraden und Ebenen werden simuliert, Geogebraprogramme liefern auch die Abstände. (GEO) | |
| Tetraeder |
Wie können vier Punkte auf einer Kugeloberfläche verteilt werden, so dass sie den größten Abstand voneinander haben. Am Beispiel von Methan wird es gezeigt. (GEO) | |
| Sinuskurve |
Wie wird eine Sinusfunktion am Kreis erzeugt? Ein Applett macht es nachvollziehbar. (GEO) | |
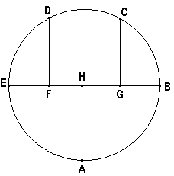 Königsberger Brückenproblem, Aufgabe von Nicole Kretschmer |
Kann man diese Figur zeichnen mit nur 3 mal absetzen?(WORD) | Download |
| Die drei berühmtesten antiken Probleme der griechischen Geometrie |
Die Quadratur des Kreises, die Winkeldrittelung und die Verdoppelung des Würfelvolumens werden auf verschiedene Wege beschrieben. Es helfen die archimedische Spirale, die Quadratrix, Winkelhaken oder verschiedene Beziehungen am rechtwinkligen Dreieck. Spannende Beweise werden geführt.(WORD),(GEO) | Download |
|
Geknickter 10 €-Schein |
Ein 10 €-Schein wird seltsam geknickt. Interessante geometrische Fragestellungen ergeben sich. (WORD),(GEO) | |
verschiedene Dreieckshalbierungen |
Die Fläche eines allgemeinen Dreiecks soll halbiert werden. Die Zerlegung erfolgt in ein kleineres Dreieck und ein Trapez (mit Konstruktionsbeschreibung), durch eine zur Grundseite parallele Linie und einer Linie, damit auch beide Umfänge gleich groß sind.(WORD),(GEO) | |
| Dreiecks- drittelung |
Die Fläche eines allgemeinen Dreiecks soll durch zwei zur Grundseite parallen Linien gedrittelt werden. Die Länge der Linien und die Abstände zur Grundseite werden ermittelt.(WORD),(GEO) | |
| Flächenteilungs- probleme |
Ob Rechtecks-,Trapez-,Fünfecksteilung oder Kreishalbierung, für jede geometrische Form wird ein interessantes Problem gelöst.(WORD),(GEO) | |
| Problem am Rechteck |
Eine Spinne zieht einen Faden in einem Rechteck, die Seitenlängen des Rechtecks werden gesucht. (WORD),(GEO),(PDF) | |
| Teildreieck im Quadrat |
Ein Eckpunkt eines Dreiecks und der Mittelpunkt eines Quadrats sind identisch. Mit wie viel Dreiecksfläche wird das Quadrat überlappt? Zwei mögliche Lösungen werden gezeigt.(WORD),(GEO) | |
| Viereck im Dreieck |
Der Flächeninhalt eines Vierecks wird in einem gleichschenklig, spitzwinkligen Dreieck gesucht. (WORD) | |
| Verkehrte Tortenschachtel |
Eine dreieckige Torte wird bebacken. Die dazu passende Schachtel hat gleiche, aber seitenverkehrte Maße. Zwei Schnitte lösen das Problem. Wie diese Schnitte verlaufen, zeigt eine Geogebraanimation.(WORD),(GEO) | |
| Linien im gleichseitigen Dreieck |
Drei Linien laufen im gleichseitigen Dreieck auf einen Punkt P zu. Die Länge einer Dreiecksseite wird bestimmt.(WORD),(GEO) | |
|
Zwei schöne Aufgaben am rechtwinkligen Dreieck |
Die Innenwinkelgröße eines rechtwinkligen Dreiecks wird gesucht, wo Um-und Inkreis eine besondere Lage zueinander haben. Ein Teil einer Kathete wird gesucht.(WORD),(GEO) | |
|
Punkte einer Pyramide im Raum |
Die Punkte werden bestimmt, wenn die Spitze der Pyramide in einer gegebenen Ebene liegt.(WORD),(GEO) | |
|
Seitenlänge eines Quadrats |
Die Seitenlänge eines Quadrats wird gesucht, wenn drei besondere Linien im Quadrat gegeben sind.(WORD),(GEO) | |
|
Konzentrische Quadrate |
Die Seitenlänge von vier konzentrischen Quadraten wird gesucht, wenn drei Flächen im Quadrat gleich sind.(PDF),(GEO) | |
|
Flächengleiches Rechteck und Quadrat |
Zwei ganzzahlige Seitenlängen von Rechteck und Quadrat sind unter bestimmten Bedingungen gesucht.(PDF),(GEO) | |
|
Gefaltetes Quadrat |
Eine Ecke eines Quadrats wird auf die gegenüberliegende Seitenkante gelegt. Es entstehen zwei Flächen, deren Verhältnis gesucht wird.(PDF),(GEO) | |
|
Vier Viertelkreise im Quadtrat |
Die gemeinsame Fläche von vier Viertelkreisen im Quadtrat wird auf vier unterschiedliche Arten berechnet.(PDF),(GEO) | |
|
Kuchenteilung |
In einem rechteckigen Kuchenstück liegt ein gleichseitiges Dreieck. Wie verläuft ein gerader Schnitt, wenn die Kuchenfläche halbiert werden soll?(PDF),(GEO) | |
|
Fünf japanische Kreise |
Japanische Studenten ordnen fünf Kreise speziell an, nur ein Radius ist bekannt. Der Radius des fünften Kreises ist gesucht, eine spannende Aufgabe. (PDF),(GEO) | |
|
Kreisring im n-Eck |
Einem n-Eck (n>2) werden In-und Umkreis zugeordnet. Wie verändert sich der Flächeninhalt des Ringes, wenn n zunimmt?(PDF),(GEO) | |
|
Flächenvergleich von regelmäßigen n-Ecken |
Regelmäßige n-Ecke werden vergrößert. Welcher Grenzwert v wird erreicht, wenn v=Bild/Original? (PDF),(GEO) | |
|
Das Haus des Nikolaus |
Der Umkreis des Nikolaushauses wird ermittelt.(PDF),(GEO) | |
|
Drei Dreiecke, ein Kreis im gleichseitigen Dreieck |
Der Flächeninhalt des größten Dreiecks wird bestimmt.(PDF),(GEO) | |
|
Gleichseitiges Dreieck gefüllt mit Kreisen |
Welchen Anteil nehmen Kreise in einem gleichseitigen Dreieck ein nimmt, wenn deren Anzahl steigt. Ein Grenzwert wird ermittelt.(PDF),(GEO) | |
|
Erster Fermat-Punkt |
Es wird gezeigt, wo der Erste Fermat-Punkt in einem Dreieck liegt.(PDF),(GEO) | |
|
Vier Viertelkreise |
Vier Viertelkreise werden zu einem Stern. Der innere Flächeninhalt wird auf vier unterschiedlichen Wegen bestimmt.(PDF),(GEO) | |
|
Fünf Quadrate |
Vier Quadrate liegen in einem fünften. Der Flächeinhalt der vier Quadrate wird bestimmt.(PDF),(GEO) | |
|
Trapez im Rechteck |
Ein Trapez liegt in einem Rechteck. Der Flächenanteil ist gesucht.(PDF),(GEO) | |
|
Halbkreis im Halbkreis |
Ein Halbkreis ist einem Halbkreis einbeschrieben. Der Durchmesser des kleineren Halbkreises wird berechnet und seine Ortskurve.(PDF),(GEO) | |
|
Größtes Quadrat und größter Kreis in einem Würfel, ein Prinz Rupert vom Rhein-Würfel zu finden |
Einem Würfel mit der Kantenlänge a=1 wird ein Quadrat und danach ein Kreis einbeschrieben. Die maximale Seitenlänge bzw. der maximale Durchmesser beider Flächen wird gesucht.(PDF),(GEO) | |
|
Zu den sechs Eichen |
Sechs Eichen sollen in einem Kreis gepflanzt werden, wobei alle 30 Abstände zwischen den Eichen ganzzahlig unterschiedlich sind. Schwierige Aufgabe mit Lösungsideen.(PDF),(GEO),(PY) | |
|
Trapezhalbierung |
Wo muss eine parallele Linie zu den beiden Parallelen im Trapez gezogen werden, damit sich dessen Flächeninhalt halbiert. Eine animierte Konstruktion löst das Problem.(PDF),(GEO) | Download |
|
Das Haus des Nikolaus aus einem Quadrat |
Ein Quadrat soll so in vier Dreiecke zerschnitten werden, dass das Haus des Nikolaus entsteht. Eine Animation zeigt die Lösung(PDF),(GEO) | Download |
|
Winkelverhältnis am Quadrat |
In einem schräg liegenden Quadrat gehen von einem Eckpunkt zwei Winkel aus. Das Verhältnis der beiden wird gesucht.(PDF),(GEO) | Download |
|
Winkel an der Spitze |
In einem spitzwinklig, gleichschenkligen Dreieck sind zwei Liniensegmente gegegeben. Der Winkel an der Spitze wird gesucht.(PDF),(GEO) | Download |
| Kurzbeschreibung | Was steht im Programm? | Download |
|
Krabbelnder Käfer |
Auf dem Planeten Beta Mathematica Zentauri will ein Käfer auf eine Kugelpyramide mit endlicher Höhe krabbeln. Diese besteht aus unendlich vielen, immer kleiner werdenden Kugeln. Der gesuchte Weg ist in einem WORD-Dokument berechnet und wird in GeoGebra simuliert. (WORD),(GEO) | |
| Schachbrett abdecken |
Wie kann man am besten ein Schachbrett mit 3 kleineren Quadraten abdecken? Ein schönes Anwendungsbeispiel für die Goldene Zahl und Kepler-Dreiecke. (WORD),(GEO) | |
| Rausschmiss verhindern |
Wie kann der Ausschluss aus einem Kurs verhindert werden? Schöne Knobelaufgabe zur Teilbarkeit von Lea Schröder. (WORD) | |
| Lottofee |
Eine Fee gibt Informationen, um die Lottozahlen der Ziehung 6 aus 49 der nächsten Woche voraussagen. Schwere Aufgabe von Sina Fenske. (WORD) | |
| Laserpointer |
Ein Laserpointer leutet in eine Grube. Nach Refexionen des Lichtstrahl treffen diese Kugeln über der Grube. Aufagbe von Michael Ulrich. (GEO), (WORD) | |
| Seile um den Äquator |
Passt eine Maus unter ein Seil hindurch, das um einen Meter länger ist als der Umfang des Äquators. (WORD) | |
| Die Hundekurve, eine Radiodrome |
Ein Hund will eine Katze fangen, indem er in jedem Moment auf die Katze zuläuft. Eine theoretische Herleitung der Hundekurve liegt als Word-Dokument vor, die Simulation übernimmt Geogebra. (WORD),(GEO) | |
| Die Uhrenkurve, eine Traktrix |
Eine Taschenuhr wird an einer Uhrenkette gezogen. Das Ende der Kette, welches nicht an der Uhr befestigt ist, sei K. Bewegt sich K auf der positiven der x-Achse nach rechts, entsteht eine Kurve, bei der für jede Tangente der Abschnitt zwischen dem Berührungspunkt und der Koordinatenachse konstant ist. Eine theoretische Herleitung der Uhrenkurve liegt als Word-Dokument vor, die Simulation übernimmt Geogebra. (WORD),(GEO) | |
| Die Tischlerlehrlingsaufgabe |
Der Tischlermeister gibt seinem Lehrling zwei Holzstücke, das eine hat ein kreirundes, dreieckiges und quadratisches Loch, das andere ein kreirundes, kreuzähnliches und quadratisches Loch. Aus drei Perspektiven kann man die Lösung jeweils erkennen.(WORD),(PDF),(GEO) | |
| Quadratzahlenbeweis |
Ist das um eins vermehrte Produkt von vier aufeinaderfolgen natürlichen Zahlen eine Quadratzahl? Der Beweis wird geführt.(WORD) | |
| Beweis mit Primzahlen |
Das Quadrat einer Primzahl vermindert um 1 ist durch 24 teilbar? Der Beweis wird geführt.(WORD) | |
| Geldbörsenproblem |
Eine Geldbörse wird gefunden, der Betrag wird mit dem Vermögen von 4 Personen verglichen. Problem von Fibonacci, die Lösung eines linearen Gleichungssystems mit 4 Unbekannten.(WORD) | |
| Letzte vier Ziffern |
Wie lauten die letzten 4 Ziffern von 77777? Lösung der Aufgabe mit den ersten 16 Potenzen von 7.(WORD) | |
| Tischtennisball- |
Eine Pyramide aus Tischtennisbällen soll gebaut werden. Wie viele TT-Bälle werden benötigt, wie hoch wird die Pyramide?(WORD) | |
| Hexe und Prinzessin am See |
Eine schöne Aufgabe, die sich mit Hilfe einer archimedischen Spirale lösen lässt. (WORD), (GEO) | |
| Zahlengewirr-das Freudenthal-Rätsel |
Eine sehr, sehr schwierige Aufgabe, 1969 von Hans Freudenthal erdacht. Das inhaltliche Erfassen und die Erstellung der Lösung dauerte mit vielen Unterbrechungen mehrere Jahre. (WORD) | |
| Alter von Schildkröten und Bauarbeitern |
Das Alter dreier Schildkröten und von Bauarbeitern soll herausgefunden werden, wenn bestimmt Bedingungen gegeben sind.(WORD) | |
| Finden einer Zahl |
Mit Hilfe von sechs Karten soll eine sechsstellige Zahl gefunden werden.(WORD) | |
| Seillänge zwischen zwei Pfosten |
Wie lang ist ein Seil zwischen zwei Pfosten, wenn man mehrere Funktionen zu Grunde legt, eine Längenberechnung von Kurven u.a. mit Integralen. (WORD),(GEO) | |
| Umkippendes Prisma |
Ein mit Wasser gefülltes gleichseitiges Prisma kippt um. Der Wasserinhalt verändert seine Form, interessante Fragestellungen werden zu diesem Problem aufgeworfen, eine Animation unterstützt die Antworten. (WORD),(GEO) | |
| Leiter an einer Wand |
Stellt man eine Leiter schräg an eine Wand, können schöne Probleme entstehen. Zwei Probleme werden gelöst. (WORD),(GEO) | |
| Zwei Bierdosenprobleme |
Bei welcher Bierfüllhöhe hat eine Bierdose den festesten Stand? Bei welcher Bierfüllhöhe und welchem Drehwinkel kann eine Bierdose schräg zum Stehen gebracht werden. Zwei Probleme werden gelöst. (PDF),(GEO) | |
| Bierdeckelproblem |
Zwei Bierdeckel werden so übereinander geschoben, dass die gemeinsame Fläche halb so groß ist, wie gesamte Fläche eines Bierdeckels. (PDF),(GEO) | |
| Drei Ziegenprobleme |
Ziegen weiden auf Grasflächen. Welche Flächen die Ziegen unter bestimmten Bedingeungen abfressen, werden betrachtet, so z.B. ein Kartesisches Oval. (PDF),(GEO),(Mathematica) | Das Zebrarätsel |
Auch Einstein Rätsel genannt, veröffentlicht mit dem angeblich von Albert Einstein stammenden Vermerk, lediglich 2 % der Weltbevölkerung könnten dieses Rätsel lösen.(PDF),(EX),(GEO) | Das Langford-Problem |
Es sind Zahlen zu finden, die jede Ziffer von 1 bis n genau zweimal enthalten, und bei denen zwischen den beiden Einsen eine andere Ziffer steht, zwischen den beiden Zweien zwei andere Ziffern, zwischen den beiden Dreien drei Ziffern usw.(PDF),(GEO) |
| Kurzbeschreibung | Was steht im Programm? | Download |
| Drei Probleme mit Leitern |
1. Gassenbreite mit sich kreuzenden Leitern, 2. Kreidelinie einer rutschenden Leiter, 3. Leiter mit davorstehender Kiste. (PDF),(GEO) |
|
| Dreieck im Rechteck |
Ein Dreieck wird über eine Winkelhalbierende in ein Rechteck gelegt und über einem bestimmten Umfang definiert. Das Seitenverhältnis des Rechtecks ist zu bestimmen.(PDF),(GEO) | |
| Fläche im Fünfeck |
In einem konvexen Fünfeck wird der Flächeninhalt eines konkaven Fünfecks berechnet, wenn die Flächen von drei Teilfiguren gegeben sind.(PDF),(GEO),(WORD) | |
| Quadrat und Parabel |
Der Flächeninhalt eines Quadrates, der sich über eine lineare Funktion und eine Normalparabel definiert, wird bestimmt.(PDF),(GEO),(WORD) | |
| Rechteck im Quadrat |
Ein Quadrat wird in zwei Rechtecke abgeteilt. Das kleinere Rechteck wird in das größere Rechteck schräg eingefügt. Gesucht ist das Verhältnis von Quadratseite zu einer Rechteckseite.(PDF),(GEO),(WORD) | |
| Halbkreis im Trapez |
Ein Halbkreis berühert drei Seiten eines Trapezes. Gesucht ist die Länge der Basislinie des Trapezes.(PDF),(GEO) | |
| Halbkreis und Trapez |
Ein Halbkreis liegt über der Grundseite eines gleichschenkligen Trapezes und schneidet die kürzere Parallele in zwei Punkten und die Schenkel in einem Punkt. Gesucht ist, in welchem Verhälhnis die Schenkel des Trapezes geschnitten werden.(PDF),(GEO) | |
| Linien im gleichseitigen Dreieck |
Von einem Punkt im gleichseitigen Dreieck gehen drei Linien zu den Eckpunkten des Dreiecks. Gesucht ist die Seitenlänge des Dreiecks.(PDF),(GEO),(WORD) | |
| Zwei Dreiecke im allgemeinen Dreieck |
Eine Winkelhalbierende teilt ein Dreieck, zwei Teildreiecke entstehen. Es das Verhältnis gesucht, mit der die Winkelhalbierende eine Seite des ursprünglichen Dreiecks teilt.(PDF),(GEO) | |
| Zwei Dreiecke im gleichseitigen Dreieck |
Zwei kongruente Dreiecke werden in einem gleichseitigen Dreieck erzeugt. Gesucht ist die Seitenlänge des gleichseitigen Dreiecks. (PDF),(GEO) | |
| Fläche eines Vierecks im Dreieck |
Ein Dreieck wird durch zwei Linien in drei Dreiecke und einem Viereck geteilt. Der Flächeninhalt des Vierecks ist gesucht.(PDF),(WORD) | |
| Zwei Linien im Dreieck |
Ein Dreieck wird durch eine Winkelhalbierende und einer Seitenhalbierenden in drei Dreiecke geteilt. Die Länge einer Linie im Dreieck ist gesucht.(PDF),(GEO) | |
| Seillänge zwischen zwei Pfosten |
Zwischen zwei Pfosten hängt ein Seil. Die Länge des Seils wird bestimmt mit Hilfe einer e-Funktion.(WORD),(PDF),(GEO) | |
| Drei Linien im Dreieck schneiden sich in einem Punkt |
Mit Hilfe des Satzes von Ceva wird ein Beweis geführt.(PDF),(GEO) | |
| Kugel im Kegel im Zylinder |
Ein Kegel ist im Zylinder einbeschrieben, im Kegel wiederum eine Kugel. Der Radius der Kugel ist gesucht.(PDF),(GEO) | |
| Diagonalenabschnitte eines Rechtecks |
Zwei gleichseitige Dreiecke sind in einem Rechteck. Bestimmte Diagonalenabschnitte werden berechnet.(PDF),(GEO) | |
| Zwei Kreise im gleichseitigen Dreieck |
Zwei Kreise sind in einem gleichseitigen Dreieck angeordnet. Die Radien der Kreise sind zu bestimmen.(PDF),(GEO) | |
| Punkt im Quadrat I |
Ein Punkt P befindet sich in einem Quadrat und von allen Eckpunkten laufen Linien zu P, wobei die Länge dreier Strecken bekannt ist. Die Länge der vierten Strecke ist gesucht.(PDF),(GEO) | |
| Punkt im Quadrat II |
Ein Punkt wird in ein Quadrat gesetzt, es entstehen vier Dreiecksflächen, deren Inhalt berechnet wird.(PDF),(GEO),(Mathematica) | |
| Normale auf Kreissehne |
Eine Normale wird auf eine Kreissehne gezeichnet, worauf sich ein Beweis anschließt. Eine Aufgabe von dem persischen Universalgelehrten al-Biruni (973-1048).(PDF),(GEO) | |
| Turmwendeltreppen |
Bei zwei gleich hohen Türmen führen außen Wendeltreppen herum. Der eine Turm ist dicker als der andere, bei gleicher Steigung der Treppen. Welche Treppe ist länger? (PDF),(GEO) | |
| Arbelos von Archimedes |
Arbelos sind Schustermesser, in deren Fläche man ganz interessante Aufgaben verstecken kann.(PDF),(GEO) | |
| Drei Kreise im gleichseitigen Dreieck |
Die Radien von drei Kreisen im gleichseitigen Dreieck werden berechnet.(PDF),(GEO) | |
| Zwei gleichseitige Dreiecke im Rechteck |
Diagonalenabschnitte in einem Rechteck mit zwei gleichseitigen Dreiecken werden berechnet.(PDF),(GEO) | |
| Vier Dreiecke im gleichseitigen Dreieck |
Die Entfernung eines Punktes auf der Grundlinie eines gleichseitigen Dreiecken wird gesucht, damit bestimmte Flächenverhältnisse eingehalten werden.(PDF),(GEO) | |
| Winkel im gleichschenkligen Dreieck |
Ein Winkel in einem gleichschenkligen Dreieck wird gesucht, schöne Aufgabe.(PDF),(GEO) | |
| Fliege im Tetraeder |
Eine Fliege sucht einen Weg, um aus einen Tetraeder zu krabbeln.(PDF),(GEO) | |
| Gefaltetes gleichseitiges Dreieck I |
Ein gleichseitiges Dreieck wird so gefaltet, dass eine Ecke auf die Grundseite gelegt wird. Es entstehen sich nicht überlappende Flächen, die gegeben sind. Welchen Flächeninhalt hatte des ursprüngliche Dreieck? Sehr schöne Geometrieaufgabe.(PDF),(GEO) | |
| Gefaltetes gleichseitiges Dreieck II |
Gleiche Aufgabe wie die vorige, nur mit anderen Flächeneinheiten.(PDF),(GEO) | |
| Gotisches Fenster |
Ein gotisches Kirchenfenster ist mit verschiedenen Kreisbögen versehen, die Basis des Fensters wird berechnet.(PDF),(GEO) | |
| Pentagon im Dreieck |
In ein Dreieck sind ein Pentagon und zwei rechtwinklige Dreiecke eingebaut. Gesucht ist das Verhältnis der Hypotenuse zur Seitenlänge des Pentagons.(PDF),(GEO) | |
| Halbkreis mit sechs Kreisen |
In einem Halbkreis befinden sich sechs weitere Kreise. Gesucht sind die Radien der Kreise. Eine weitere Sangaku-Aufgabe.(PDF),(GEO) | |
| Das Morikawa-Problem |
In dem Buch Sacred Mathematics (Japanese Temple Geometry) von Fukagawa Hidetoshi und Tony Rothmann (Princeton University) wird das Problem aus dem 19.Jahrhundert als ungelöst dargestellt. Ich fand eine Teillösung, Andreas Grieser, Greifswald, sogar eine Gleichung 20.Grades, die, numerisch berechnet, die minimale Seitenlänge eines Quadrates unter zwei Kreisen angibt.(PDF),(GEO),(Mathematica) | |
| Zwei Kreise über einer Sehne |
Kittas Double-Locked-Problem wird gelöst.(PDF),(GEO),(Mathematica) | |
| Weg auf einem Kegel ohne Anstieg |
Schöne Extremwertaufgabe, bei der der kürzeste Weg auf einem Kegelmantel bestimmt wird.(PDF),(GEO) | |
| Rechteck und zwei Halbkreise |
Aufgabe von Catriona Agg, bei der der Flächeninhalt eines Rechtecks bestimmt werden soll.(PDF),(GEO) | |
| Zwei Quadrate im Trapez |
Extremwertaufgabe, bei der zwei Quadrate in einem Trapez einbeschrieben sind und eine maximale Strecke gesucht wird.(PDF),(GEO) | |
| Drei Quadrate im Dreieck |
Drei Quadrate, deren eine Seite jeweils auf einer Dreicksseite liegt, werden einem Dreieck einbeschrieben. Die nicht von den Quadraten bedeckte Fläche wird berechnet.(PDF),(GEO) | |
| Der Zauberpunkt |
An einem Kreis gibt es es eine Tangente und eine Passante. In dem Kreis gibt es genau einen Punkt, so dass zwei Strecken, immer die gleiche Länge besitzen.(PDF),(GEO) | |
| Fläche des Hexagons |
In einem Hexagon sind drei Streckenlängen gegeben. Der Flächeninhalt des Hexagons wird berechnet.(EX),(PDF),(GEO) | |
| Varignon-Parallelogramm |
Ein Varignon-Parallelogramm wird so angelegt, dass es neben dem halben Flächeninhalt auch noch den halben Umfang des konkaven Vierecks hat.(PDF),(GEO) | |
| Rollendes Dreieck |
Im Innern eines Quadrats rollt ein Dreieck mit halber Quadratseitenlänge um dessen vier Seiten. Die Länge der Ortskurve eines Dreieckspunktes wird berechnet und die Bewegung simuliert.(PDF),(GEO) | |
| Spirale aus Streckenzügen |
Die Länge einer Spirale aus Streckenzügen und der dazugehörigen archimedischen Spirale wird berechnet.(PDF),(GEO) | |
| Euler-Ziegel |
Die kleinsten Euler-Ziegel unter 1,0 m Kantenlängen werden berechnet.(PY),(PDF),(GEO) | |
| Fläche Viereck aus Diagramm |
Aus einem Niederschlagsdiagramm auf Sumatra wird ein Viereck konstruiert, dessen Flächeninhalt bestimmt wird.(PDF),(GEO) | |
| Fibonacci-Winkel |
Drei Winkelgrößen werden aus einem 8x1 Raster aufsummiert. Ein verblüffendes Ergebnis entsteht.(PDF),(GEO) | |
| Winkel zwischen zwei Quadraten |
Ein Winkel zwischen zwei schräg gestellten wir berechnet.(PDF),(GEO) | |
| Punkte auf Raster |
Ganzzahlige Koordinaten auf einem Raster werden zur Bestimmung der Kreiszahl π genutzt. Ein Geogebra-Programm simuliert die Situtionen.(GEO) | |
| Gerechte Flächenteilung im Fünfeck |
Ein Fünfeck wird in einem Viertelkreis einbeschrieben. Vier Dreiecke werden darin festgelegt. Wann ist die Summe je zweier Dreiecke gleich groß bzw. wann wird sie maximal.(PDF),(GEO) | |
| Zwei überlappende Kreise |
Zwei Kreise überlappen sich, zwei interessante Fragestellungen entstehen daraus.(PDF),(GEO) | |
| Drei Trapeze im Trapez |
Drei Trapeze mit gleichem Flächeninhalt werden in ein Trapez eingefügt, gesucht ist der Flächeninhalt eines der drei Trapeze.(PDF),(GEO) | |
| Abgeschnittene Ecke eines Würfels |
Ein Satz von Johann FAULHABER (1580-1635) wird bewiesen.(PDF),(GEO) | |
| Yin und Yang |
Yang soll in zwei kongruente Flächen durch eine Linie zerlegt werden. Wie diese aussieht, wird gezeigt.(PDF),(GEO) | |
| Tangente an zwei Kreise im Quadrat |
In einem Quadrat liegen ein Halbkreis und ein Viertelkries an einer gemeinsamen Tangente. Die Seitenlänge des Quadrats ist gesucht.(PDF),(GEO) | |
| Maximale Schenkellänge eines gleichschenkligen Dreiecks |
Es wird gezeigt, wie lang die Basis eines gleichschenkligen Dreiecks sein muss, damit der Flächeninhalt maximal wird.(PDF),(GEO) | |
| Trapez und Viertelkreis im Rechteck |
Es wird gezeigt, wo ein Punkt auf einer Kreistangente an dem Viertelkreis liegen muss, damit der Flächeninhalt eines Trapezes in einem Rechteck maximal wird.(PDF),(GEO) | |
| Zwei Quadrate im Kreis |
Zwei Quadrate sind in einem Kreis einbeschrieben. Gesucht ist der Umfang des Kreises.(PDF),(GEO) | |
| Zwei sich schneidende Kreise |
Der Schnittpunkt zweier sich schneidender Kreise wird gesucht.(PDF),(GEO) | |
| Unzugängliche Strecke im Dreieck |
Eine Aufgabe von dem wunderbaren Mathematiklehrer Wolfgang Hegenwald, Schönebeck, von 1962. Eine nicht zu messende Strecke wird über Winkelbeziehungen berechnet.(PDF),(GEO) | |
| Ein fast gleichseitiges Dreieck |
Eine Waldfläche wird berechnet aus einem fast gleichseitigen Dreieck. Eine diophantische Gleichung muss gelöst werden. (PDF),(GEO),(PY),(Mathematica) | |
| Vier Quadrate stützen ein Quadrat |
Die Fläche eines Quadrates ist gesucht, wobei die Seitenlängen der stützenden Quadrate gegeben sind. (PDF),(GEO) | |
| Steigung der Winkelhalbierenden |
Zwei Geraden mit den Steigungen 1 und 3 sind gegeben. Die Steigung der Winkelhalbierenden wird bestimmt. (PDF),(GEO) | |
| Ein gleichschenkliges Dreiecksproblem |
Ein Winkel wird in einem Dreieck berechnet, das zwei gleichschenklige Dreieck beinhaltet. (PDF),(GEO) | |
| Zwei Kreise im Rechteck |
Zwei Kreise sind im Rechteck, der Abstand der Mittelpunkte ist gesucht. (PDF),(GEO) | |
| Strecke am Viertelkreis |
Eine Strecke am Viertelkreis ist gesucht. (PDF),(GEO) | |
| Gefalteter Halbkreis |
Ein Halbkreis wird so gefaltet, dass ein Peripheriepunkt den Durchmesser in zwei Strecken teilt. Die Länge der Faltnaht ist gesucht. (PDF),(GEO) | |
| Halbkreis im Viertelkreis |
Ein Halbkreis ist einem Viertelkreis einbeschrieben. Welcher Bruchteil des Viertelkreises ist rot? (PDF),(GEO) | |
| Winkel im Viereck |
Drei Vielfache eines Winkels im Viereck sind gegeben, der einfache Winkel ist gesucht. (PDF),(GEO) | |
| Drei Kreise im Kreis mit gleichseitigem Dreieck |
Drei Kreise sind einem Kreis einbeschrieben, ebenfalls ein gleichseitiges Dreieck, die Restfläche ist gesucht. (PDF),(GEO) | |
| Verhältnis paralleler Seiten im Trapez |
Die Diagonalen teilen ein Trapez in vier Flächen, deren Inhalte gegeben sind. Das Verhältnis der parallelen Seiten ist gesucht. (PDF),(GEO) | |
| Drei Quadrate im Halbkreis |
Drei Quadrate werden einem Halbkreis einbeschrieben. Ein Beweis über eine gerade Linie soll geführt werden. (PDF),(GEO) | |
| Beweis Winkel im Quadrat ist 60° |
In einem Quadrat wird unter betsimmten Bedingungen ein Winkel definiert. Es ist zu beweisen, dass dieser Winkel 60°groß ist. (PDF),(GEO) | |
| Drei Quadrate im gleichseitigen Dreieck |
Einem gleichseitigen Dreieck werden drei Quadrate einbeschrieben. Die Seitenlänge des Dreiecks wird bestimmt. (PDF),(GEO) | |
| Vier Halbkreise im Quadrat |
Die Restfläche von vier Halbkreisen im Quadrat wird berechnet. (PDF),(GEO) | |
| Verhältnis zweier Dreiecke im Viereck |
Ein Viereck wird in vier Dreiecke zerlegt, das Verhältnis zweier Dreiecke wird gesucht. Verschiedene Seienlängen sind dann gegeben. Schöne Aufgabe mit goldenen Dreiecken.(PDF),(GEO) | |
| Sehnenabschnitt in zwei Kreisen |
Ein Sehnenabschnitt zwischen zwei Kreisen wird gesucht.(PDF),(GEO) | |
| Winkel im Dreieck im Quadrat |
In ein Quadrat ist ein Dreieck einbeschrieben, ein Winkel ist gegeben, die anderen beiden werden gesucht. (PDF),(GEO) | |
| Zwei Winkel an Tangenten und Sehnen |
Zwei Kreise berühren einander. Es wird ein Viereck aus je zwei Tangenten und Sehnen gezeichnet, die Größe zweier Innenwinkel des Vierecks wird gesucht.(PDF),(GEO) | |
| Zwölf-Grad-Konstruktion |
Die Konstruktuionsbeschreibung eines 12-Grad-Winkels erfogt in 13 Schritten.(PDF),(GEO) | |
| Beweise im allgemeinen Dreieck |
Vier Beweise werden im allgemeinen Dreieck geführt.(PDF),(GEO) | |
| Drei sich berührende Kreise |
Drei Kreise liegen auf einer Geraden und berühren sich jeweils. Der Radius des kleinsten Kreises ist gesucht.(PDF),(GEO) | |
| Beweis, dass zwei Tangentenabschnitte gleich lang sind. |
Zwei Kreise sind einem Kreis einbeschrieben. Der Beweis, dass zwei Tangentenabschnitte gleich lang sind, wird geführt. (PDF),(GEO) | |
| Dreieck im Quadrat und Rechteck |
Einem Quadrat und Rechteck wird ein Dreieck einbeschrieben. Es entstehen drei nichtbedeckte Flächen, den Inhalt bekannt ist. Der Flächeninhalt des einbeschriebenen Dreiecks wird gesucht.(PDF),(GEO) | |
| Treffen sich zwei Rechtecke |
Ein Rechteck hat den doppelten Flächeninhalt, das andere den doppelten Umfang des anderen. Die Seitenlängen beider Rechtecke sind gesucht.(PDF),(GEO),(PY) | |
| Dreieck und Halbkreis |
Eine Dreiecksseite wird in einem Halbkreis eingebunden, sie wird berechnent.(PDF),(GEO) | |
| Seite eines Dreiecks mit zwei Winkelhalbierenden |
Eine Dreiecksseite wird gesucht, wenn zwei Winkelhalbierende gegeben sind.(PDF),(GEO) | |
| Sehne im Kreis mit gleichschenkligem Dreieck |
Eine Sehne im Kreis wird gesucht, dem ein gleichschenkliges Dreieck einbeschrieben worden ist.(PDF),(GEO) | |
| Strecke mit zwei Geraden und zwei Kreise |
Eine Strecke wird berechnet, bei der zwei Geraden und zwei Kreise eine Rolle spielen.(PDF),(GEO) |
| Kurzbeschreibung | Was steht im Programm? | Download |
| Herzkurve |
Die Fläche einer Herzkurve wird mit drei Funktionen bestimmt.(PDF),(GEO) | |
| Funktion dritten Grades und Sinusfunktion |
Funktionsgleichungen sollen unter bestimmten Bedingungen bestimmt werden.(PDF),(GEO) |
| Japanische Tempelgeometrie, bemalte Holztafeln (Sangaku) dienten als Vorlage |
Fünf Kreise sind in einem Quadrat speziell angeordnet, der Radius der Kreise ist gesucht.(PDF),(GEO) | |
| Zwei Halbkreise im Kreis |
Schöne Aufgabe von Presh Talwalkar, der die Fläche eines Kreises mit der Summe der Flächen von zwei Halbkreisen vergleicht. Eine Geogebra-Animation zeigt die Lösung.(PDF),(GEO) | |
| Beweis 1 |
Quadrat unter zwei Kreisen.(PDF),(GEO) | Download |
| Beweis 2 |
Drei kleine Kreise zwischen zwei großen Kreisen.(PDF),(GEO) | Download |
| Beweis 3 |
Kreis zwischen drei Kreisen.(PDF),(GEO) | Download |
| Beweis 4 |
Sehne und geometrisches Mittel.(PDF),(GEO) | Download |
| Beweis 5 |
Drei Sehnen und vier Kreise.(PDF),(GEO) | Download |
| Beweis 6 |
Vier kleine Kreise in drei große Kreise.(PDF),(GEO) | Download |
| Beweis 7 |
Vier Kreise im Halbkreis.(PDF),(GEO) | Download |
| Beweis 8 |
Fünf Kreise im Kreis.(PDF),(GEO) | Download |
| Beweis 9 |
Zehn kleine Kreise in zwei große Kreise.(PDF),(GEO) | Download |
| Beweis 10 |
Fünf Kreise in zwei große Kreise.(PDF),(GEO) | Download |
| Beweis 11 |
Zwei Kreise in zwei rechtwinkligen Dreiecken.(PDF),(GEO) | Download |
| Beweis 12 |
Drei Kreise und ein rechtwinkliges Dreieck.(PDF),(GEO) | Download |
| Beweis 13 |
Zwei Kreise und ein gleichschenkliges Dreieck im Kreis.(PDF),(GEO) | Download |
| Beweis 14 |
Sieben Kreise im Kreis.(PDF),(GEO) | Download |
| Beweis 15 |
Fünf Kreise im Kreis.(PDF),(GEO) | Download |
| Beweis 16 |
Vier Kreise und zwei Bögen im Kreis.(PDF),(GEO) | Download |
| Beweis 17 |
Vier Kreise und zwei Halbkreise im Rechteck.(PDF),(GEO) | Download |
| Beweis 18 |
Vier Kreise im Kreis.(PDF),(GEO) | Download |
| Beweis 19 |
Vier Kreise im Kreis.(PDF),(GEO) | Download |
| Beweis 20 |
Sechs Kreise im Quadrat, zwei Kreise um das Quadrat.(PDF),(GEO) | Download |
| Beweis 21 |
Fünf Kreise im Rechteck.(PDF),(GEO) | Download |
| Beweis 22 |
Fünf Kreise im Quadrat.(PDF),(GEO) | Download |
| Beweis 23 |
Fünf Kreise im Quadrat.(PDF),(GEO) | Download |
| Beweis 24 |
Sechs Kreise am gleichseitgen Dreieck.(PDF),(GEO) | Download |
| Beweis 25 |
Zwei Kreise und zwei Viertelkreise im Quadrat.(PDF),(GEO) | Download |
| Beweis 26 |
Zwei Kreise und zwei Viertelkreise mit zwei Quadraten.(PDF),(GEO) | Download |
| Beweis 27 |
Sechs Kreise und ein gleichschenkliges Dreieck im Kreis.(PDF),(GEO) | Download |
| Beweis 28 |
Drei Kreise und ein Tangentenabschnitt.(PDF),(GEO) | Download |
| Beweis 29 |
Zwei Kreise im Rechteck.(PDF),(GEO) | Download |
